ГЛАВА VI
«Несчастный случай»
Бытует мнение, что жизнь человеческая состоит из полос «везения» и «невезения» и что добивается успеха только тот, кто умеет максимально использовать шанс, предоставленный ему судьбой в периоды везения, и «затаиться» и ждать в периоды «невезения». Кто из нас не испытывал чувства безысходности, попадая в жизненную полосу неудач и укрепляясь в мысли о том, что беда не приходит одна? Правда, для одних «невезение» — это именно то, что для других выглядит совсем иначе. Оценка жизненных ситуаций, как правило, вещь субъективная. Другое дело — игра.
В любой игре оценка ее результатов определяется предварительным соглашением и в следствии этого ее можно считать в какой-то мере объективной. Во всяком случае, результатом каждого тура игры являются вполне определенные ответы — либо «выиграл», либо «проиграл». Кажется вполне резонным вопрос, который может задать математикам неискушенный читатель о том, насколько длинной может быть серия, состоящая только из слов «выиграл»; или серия, состоящая из слов «проиграл». Могут ли математики ответить на этот вопрос? Каждый из нас, наверное, согласится, что ответ на этот вопрос не может быть однозначным. Как говорится, какой вопрос — такой и ответ, А вопрос этот касается той области человеческих знаний, в которой не существует однозначных ответов, а сами ответы должны содержать значительную долю неопределенности, типа «это, в принципе, возможно, но маловероятно» или «с большой степенью вероятности должно произойти то-то и то-то». Ответы такого типа вовсе не исключают альтернативных исходов, и даже в какой-то степени их допускают, но при этом дают оценку вероятности того или иного исхода событий.
В качестве примера рассмотрим возможность возникновения длинной серии одинаковых результатов при многократном подбрасывании монеты. Каждое из подбрасываний приводит либо к результату О (выпал орел), либо Р (выпала решка). Допустим, что по условию эксперимента подбрасывание происходит до тех пор, пока не выпадет первая решка. Таким образом, результатом нашего эксперимента может быть одна из следующих серий:
Р, ОР, ООР, ОООР, ООООР, ОООООР, ООООООР...,
то есть серии, в которых буква О встречается О, 1, 2, 3, 4, 5, 6… раз. С какой вероятностью может встречаться каждая из этих серий, видно из приведенной ниже Таблицы 5 и графика, представленного на Рис. 5.
Таблица 5. Вероятности различных серий при подбрасывании монеты.
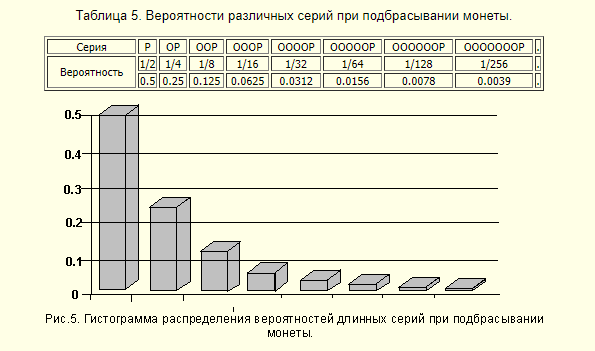
Эти вероятности легко вычислить, если принять во внимание, что в каждом броске выпадение орла и решки равновероятны; и поэтому вероятность каждого из этих двух возможных исходов равна 0,5 (50%). Отсюда, в частности, следует, что вероятность выпадения серии ООООР равняется
0.5х0.5х0.5х0.5х0.5=0.03125,
то есть около 3%.
Может ли встретиться, например, длинная серия выпадения подряд 9 орлов ОООООООООР? Согласно вышеприведенному правилу подсчета, вероятность такого исхода равна
0.5 х 0.5 х 0.5 х 0.5 х 0.5 х 0.5 х 0.5 х 0.5 х 0.5 х 0.5 = 0.0009777,
что составляет около 0,1%. Следовательно, такая серия возможна, но очень маловероятна, может встретиться в среднем 1 раз в каждых 1000 попытках получить такую серию. Если же такая серия в ваших экспериментах встретится существенно чаще, то это будет означать, что либо в этих экспериментах не все очень чисто, либо вас преследует злой или счастливый рок, в зависимости от того, на что вы поставили: на орла или на решку.
Вернемся теперь к игре в ЛОТТО. В предыдущих главах мы рассмотрели способы подсчета вероятностей угадывания 4-х, 5-ти и 6-ти чисел в каждом отдельном билете. Будем считать эти вероятности известными и обозначим их соответственно P4 P5, и P6. Попытаемся теперь ответить на следующий вопрос. Какова вероятность длинной серии неудач, если ставить в каждом туре на одну и ту же комбинацию? Пусть, например, вы выбрали для себя заветную комбинацию из 6, 7 или 8 чисел и решили каждый тур покупать по одному билету и из тура в тур в этом билете отмечать именно эту комбинацию. Вы набрались терпения и не отчаиваетесь, если вам не повезет в первом, втором, третьем и т.д. турах. Но должно же когда-нибудь повезти? А если серия неудач будет длиться год, два, три? Что это — несчастный случай или закономерность? Вы сами можете ответить на этот вопрос.
Сначала найдем вероятность неудачи в первом туре. Так как вы потерпели неудачу, то значит, вы не угадали 6 чисел
(вероятность 1 — P6), не угадали 5 чисел (вероятность 1-P5) и не угадали 4 числа (вероятность 1- P4). Вероятность этого события для одного тура игры
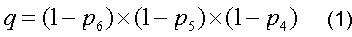
Формула (1) определяет вероятность «несчастного» случая только для одного тура. А если эта серия неудач продолжается подряд в течение m туров, то есть выпала серия
где Н — неудача, У- угадал или 6, или 5, или 4, числа, то вероятность этой серии, как нетрудно догадаться, будет равна
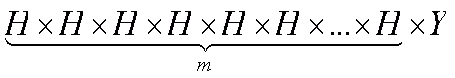
Эта формула определяет вероятность того, что серия неудач будет точно длиной в m туров.
Применим эти формулы для оценок вероятности некоторой гипотетической, но вполне реальной ситуации. Предположим, что вы решили играть по простой схеме и каждый тур покупать по 100 билетов (на 3000 рублей).
Если P4, P5 и P6 вероятности угадывания соответственно 4-х, 5-ти и 6-ти чисел, тогда вероятность, что не будет угадана ни одна из этих комбинаций в 100 билетах равна
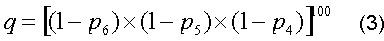
Согласно Таблице 4, =0,0096862, =0,00001845 и =0,0000000715. Подставив эти значения в (3), получим q=0,377. В Таблице 6 приведены вероятности для различных серий по турам игры при рассматриваемых условиях, вычисленные по формуле (2).
Таблица 6. Вероятности различных серий по турам при условии заполнения 100 билетов по простой схеме в каждом туре*

*H – не угадано ни одной комбинации в каждом из 100 билетов. У – угадана хотя бы одна комбинация в одном из 100 билетов.
Из этой же таблицы видно, что вероятность длинных серий неудач при этих условиях очень быстро уменьшается с ростом длины серии. В частности, например, вероятность потерпеть неудачу подряд в семи турах, согласно Таблице 6, меньше 0,1%, и если такое с вами случится, то вы можете считать, что имел место «несчастный случай». Формула (2) для определения вероятности длинных серий удач и неудач известна математикам очень давно и называется формулой Паскаля. Для решения задач подобного рода существует и другая полезная формула, которая называется формулой Бернулли. Она позволяет найти вероятность того, что в результате участия в n турах игры количество туров без единого выигрыша будет равно m
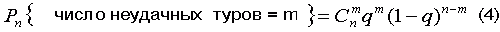
Проиллюстрируем, как можно использовать формулу (4) для подсчета вероятностного числа неудачных туров. Пусть, как и выше, в каждом туре заполняется 100 билетов по простой схеме и q=0.377, а полное число сыгранных туров n=4.
1) Найдем вероятность того, что во всех четырех турах нас постигнет неудача (m=4), то есть не будет ни разу угадана ни одна комбинация
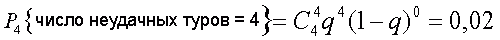
так как
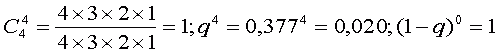
Следовательно вероятность потерпеть неудачу во всех четырех турах равна 0.02 или составляет 2%.
2) Определим вероятность угадать хотя бы одну комбинацию в одном единственном туре:
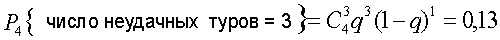
так как
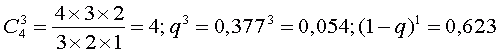
то есть составляет 13%.
3) Вероятность двух угаданных туров из четырех сыгранных равна:
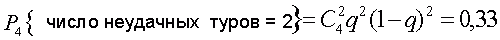
так как
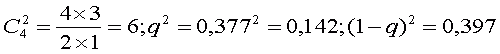
или составляет 33%.
4) Вероятность трех удачных туров
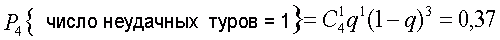
так как

или составляет 37%.
5) И, наконец, вероятность того, что во всех четырех турах будет угадана хотя бы одна комбинация, равна
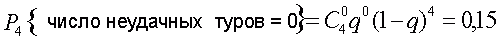
так как
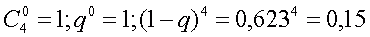
что составляет 15%
Легко убедиться, что сумма всех этих вероятностей
2%+13%+33%+37%+15%= 100%.