ГЛАВА V
Выиграть побольше или… проиграть поменьше?
Любой участник игры прежде чем приступать к игре и в процессе ее должен для себя ответить на ряд вопросов: стоит ли играть, какой стратегии игры придерживаться, как часто и как долго играть и т.д. Один из первых и, возможно, один из наиболее важных вопросов, на которые приходится отвечать — это сколько билетов покупать: много или мало. Что предпочтительней — купить много билетов и в каждом из них отметить ровно по шесть чисел, то есть принять простую систему игры, или лучше купить мало билетов и в каждом из них отмечать больше, чем шесть чисел, то-есть воспользоваться развернутой системой? Попытаемся ответить на этот очень важный вопрос, имея, конечно, ввиду, что универсальных ответов и гарантированных рецептов в мире, где законом является случайность и вероятность, не существует. Можно лишь говорить о средних или о наиболее вероятных значениях. Если утверждается, что средний рост мужчины в городе N -175 см, это вовсе не означает, что первый же встретившийся мужчина будет иметь именно такой рост. Точно также, если мы скажем, что средняя величина выигрыша, приходящаяся на каждые затраченные 30 руб., по системе игры А больше, чем по системе Б, это вовсе не означает, что все игроки придерживающиеся системы А, выиграют больше, чем те, кто придерживаются системы Б, хотя в среднем это правило выполняется.
Выше мы провели полный анализ простой системы игры. Попытаемся теперь провести аналогичный анализ для развернутой системы. Итак, вы купили билеты и, воспользовавшись развернутой системой игры, например, заплатили 210 рублей, отметив в билете 7 чисел. Теперь вы хотите оценить величину среднего выигрыша, приходящуюся на каждые 30 руб., чтобы сравнить ее с аналогичным значением для простой системы игры.
Начнем с анализа выигрышей I категории, когда из 7 отмеченных вами чисел 6 попадает в заветную «счастливую» область, а одно число — в «несчастливую» область.
Общее число семерок, которые можно образовать из 49 чисел
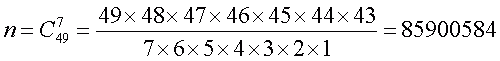
Число же способов, которыми можно получить «счастливые» шестерки, равно произведению числа способов, которыми любые шесть чисел из выбранной семерки могут попасть в «счастливую» область, на число способов, которыми оставшееся одно число из семерки можно разместить в «несчастливую» область из 43 не заштрихованных клеток билета:
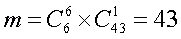
Вероятность выигрыша I категории, следовательно, равна
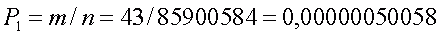
В отличие от простой системы, если вы угадали 6 чисел в развернутой системе при семи отмеченных числах, каждый выигрыш I категории сопровождается одновременно шестью выигрышами II категории (см. Таблицу 2). Действительно, вместо каждого из чисел, попавших в «счастливую» область, по очереди можно вставить то единственное число, которое попало в «несчастливую» область и, следовательно, таких комбинаций — 5 «счастливых» чисел + 1 «несчастливое» число — можно составить всего 6. Таким образом, если вы угадали 6 чисел, то средний выигрыш, приходящийся на 1 билет с 7 отмеченными числами, будет равен
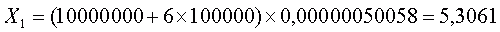
то есть составит около 5 руб. 30 копеек. Здесь, как и ранее, принято, что выигрыш II категории оценивается в 100 тыс. руб., I категории -10 млн. рублей.
Оценим теперь среднюю величину выигрыша при пяти угаданных числах, когда 2 числа из семи отмеченных попадут в «несчастливую» область, а остальные 5 — в «счастливую» область. Всего количество комбинаций, благоприятных для такого исхода игры:
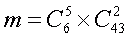
где
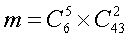
Следовательно, m = 6 х 903 =5418 благоприятных комбинаций и вероятность такого исхода
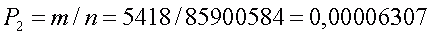
Если угадано пять чисел, при семи отмеченных числах, то, как показано на Рис.4, можно образовать 2 выигрышных комбинации II категории и 5 выигрышных комбинаций III категории.
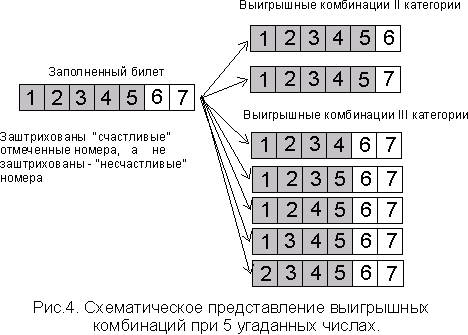
В результате средняя величина выигрыша на билет с семью отмеченными числами при 5 угаданных числах и сформулированных ранее условиях будет равна (в руб.)
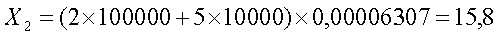
И, наконец, рассмотрим ситуацию, когда угадано 4 числа из семи отмеченных.
Вероятность угадать четыре числа будет равна
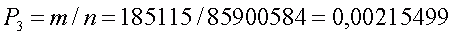
поскольку, в этом случае количество благоприятных для выигрыша комбинаций
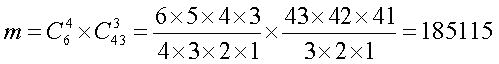
Если угаданы четыре числа, то из остальных трех «несчастливых» отмеченных надо выбрать пару чисел, которые при добавлении к «счастливой» шестерке образуют выигрышную комбинацию III категории. Поскольку из трех чисел можно образовать три различные пары, то можно сформировать 3 различные выигрышные комбинации III категории (см. Табл. 2). Таким образом, средний выигрыш на один заполненный билет в этом случае будет равен
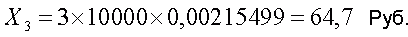
В итоге суммарный средний выигрыш, приходящийся на один билет с семью отмеченными числами, составляет
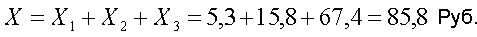
Учитывая теперь, что стоимость такого билета составляет 210 рублей, можно прийти к выводу о том, что на каждые затраченные 30 рублей средний выигрыш составляет
85,8 / 7 = 12,2 руб.
или ровно столько же, как и в простой системе. Аналогичные расчеты можно провести для развернутой системы в случае, когда число отмеченных чисел равняется 8 или 9. Результаты таких расчетов сведены в общую Таблицу 3. Как видно из последней строки этой таблицы, количество отмеченных чисел в билете не влияет на среднюю величину выигрыша, приходящуюся на каждые затраченные 30 рублей, и при принятых выше размерах ставок составляет 12,2 руб. или, другими словами, и в простой системе, и в развернутой системе при любом количестве отмеченных чисел в билете суммарная средняя доля прибыли, идущая на покрытие выигрышей I, II и III категорий, всегда одинакова и зависит только от установленных ставок этих выигрышей. При принятых нами выше значениях ставок 10 млн., 100 тыс. и 10 тыс. руб. эта доля составляет 41%.
Таким образом, средняя величина выигрыша на каждый затраченный рубль и в простой, и в развернутой системе, независимо от того, сколько чисел отмечено в билете, одинаковы. То есть в этом смысле все равно, потратить ли 210 рублей, купив 7 билетов и в каждом из них отметить 6 чисел, или купить один билет и отметить в нем 7 чисел, заплатив те же 210 рублей, Действительно ли нет никакой разницы между этими двумя системами? И какой же в этом случае был смысл усложнять условия игры, вводя развернутую систему?
Оказывается, различие между этими двумя системами существует, и это иллюстрируют результаты расчета, приведенные в Таблице 4. В этой таблице приведены вероятности выигрышей каждой из категорий и средний выигрыш, приходящийся на каждые 3 тысячи затраченных рублей при разном количестве отмеченных чисел. Средний выигрыш, конечно, не совпадает с суммой выигрыша каждого конкретного игрока, а является некоторой статистической характеристикой для большого количества участников игры. Если внимательно присмотреться к таблице, то можно заметить, что по мере увеличения количества отмеченных чисел в билете средние выигрыши в I и II категориях быстро возрастают приблизительно на 10% и20% соответственно при добавлении одного отмеченного числа, в то время как средняя величина выигрышей III категории уменьшается приблизительно на 5%. Что же касается вероятностей выигрышей при фиксированной затраченной сумме денег на покупку билетов (в Таблице 4 на 3000 руб.), то, она, для выигрышей I категории остается почти неизменной, в то время, как для II и III категорий быстро уменьшается.
Таким образом, при увеличении количества отмеченных чисел в билете в целом, выигрыши становятся крупнее, но вероятность более мелких выигрышей при этом резко уменьшается. Такова жизнь, в которой за все приходится платить!
Так какую же систему игры избрать, простую или развернутую? И если развернутую, то сколько чисел лучше отметить в билете? Можно ли ответить на эти вопросы? Можно, но только в том смысле, что нет универсального ответа на этот вопрос. Глядя на Таблицу 4, вы видите весь «товар» целиком, а дальше выбирайте сами, ориентируясь на свои вкусы и возможности. Если вы не любите сильно рисковать и считаете, что лучше иметь «синицу в руках, чем журавля в небе», то вам, по-видимому, ближе простая система игры, в противном случае, если вы стремитесь только к крупному выигрышу, то для вас предпочтительнее развернутая система игры.