ГЛАВА IV
Сколько стоит вероятность
До сих пор мы почти не касались финансовой стороны игры, определяющей ставки и величину выигрыша. Вполне естественно задать вопрос, в какой мере вероятность угадывания шести, пяти или четырех отмеченных чисел определяет справедливые условия игры? Какие условия игры можно считать справедливыми, а какие нет? В какой мере можно рассчитывать на выигрыш и т.д.?
Прежде чем перейти к обсуждению этого вопроса, следовало бы уточнить понятие справедливой игры. Это понятие сильно зависит от способа ее организации. Если эта игра не является общественной и для ее организации и обслуживания нет необходимости вкладывать дополнительные финансовые средства, то справедливыми следовало бы, по-видимому, считать условия, при которых средняя величина выигрыша для каждого из ее участников строго равнялась бы сумме вложенных денег. То есть, сколько вложил — столько в среднем и выиграл. Конечно, такая формулировка справедливости, на первый взгляд, может показаться абсурдной, поскольку лишает игру элемента неожиданности, связанного либо с большим выигрышем, либо с полным разорением.
Однако это вовсе не так. Когда мы говорим, что средняя величина выигрыша равняется количеству вложенных денег, это вовсе не означает, что в результате игры каждый игрок получит столько-то и столько-то. Например, если в игре участвуют три игрока А, Б и В, вложившие в игру, например, по 1000 рублей, то может оказаться, что игрок А выиграет 50 рублей, игрок Б -2500 рублей, а игрок В — 450 рублей, а каждый из них выиграет в среднем по (50+2500+450)/3=1000 рублей. Именно в отклонении от среднего значения для игроков А, Б и В и будет состоять элемент везения или невезения.
Однако сформулированное выше правило справедливости игры для организаторов общественных игр, какими бы они ни были бескорыстными, очевидно является неприемлемым. Определенную долю ставок организаторы вынуждены присваивать, чтобы оплатить расходы на организацию игры, её рекламу, инвентарь и персонал, не говоря уж о налогах и благотворительных акциях. Это присвоение части ставок должно учитываться при установлении правил игры. Поэтому справедливое условие общественной игры можно сформулировать следующим образом: средняя величина выигрыша для каждого участника должна равняться количеству вложенных денег минус средства, которые присваиваются организаторами игры на цели, перечисленные выше.
Предположим, что на эти цели расходуется 40 процентов ставок. Тогда, если стоимость билета составляет 30 рублей, при справедливых условиях игры средняя величина выигрыша должна равняться 12 рублям. Из чего же складывается эта величина? Вот на этот вопрос мы и попытаемся сейчас ответить.
Когда вы покупаете билет и отмечаете шесть заветных чисел, то, конечно, в первую очередь надеетесь получить выигрыш I категории, то есть угадать все шесть цифр и получить свои миллионы. Вы и без всякой математики, конечно, знаете, что шанс угадать все шесть чисел очень не велик, и поэтому в душе надеетесь получить хотя бы выигрыш II категории (угадать пять чисел), ну в худшем случае — выигрыш III категории. Итак, вы купили билет, отметили шесть чисел и ждете решения судьбы. Какой средний выигрыш вас ждет?
Давайте попробуем его оценить вместе. Начнем с оценки среднего выигрыша I категории. Все игровое поле состоит из 49 чисел и делится на две области: «счастливую», включающую шесть заветных чисел, и «несчастливую», включающую остальные 43 числа. Случайное событие А, на которое вы рассчитываете в данном случае, состоит в том, что вся ваша шестерка точно попадет в заветную «счастливую» область — и для этого есть только одна единственная возможность. Таким образом, число благоприятных для А исходов m=1. Неблагоприятных же для А исходов — великое множество: для этого достаточно, чтобы хотя бы одно, отмеченное вами число попало в «несчастливую» область. При этом общее число всех возможных исходов совпадает с числом способов, которыми можно выбрать шесть чисел из 49, и равно
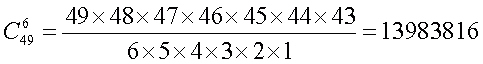
Согласно сформулированному нами ранее правилу подсчета вероятности, для ее нахождения надо поделить m на n.
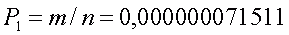
Не правда ли, шокирующе маленькая величина? Может быть, мы ошиблись? Нельзя ли ее определить другим способом? Можно, но, к сожалению, результат будет таким же! Тем не менее, представляет интерес и другой способ подсчета вероятности. Он достаточно прост и состоит в последовательном определении вероятности угадывания очередного числа. Когда мы отмечаем в билете первое число, то вероятность, что это число попадет в «счастливую» область, равна 6/49. После того, как мы угадали первое число, в «счастливой» области остается 5 чисел, а всего чисел 48, и поэтому вероятность, что второе число также попадет в «счастливую» область, будет равна 5/48. Продолжая аналогичную цепь рассуждений, найдем вероятность угадывания третьего числа — 4/47, четвертого — 3/46 и т.д. Таким образом, вероятность угадать все шесть чисел равна

Покончив с подсчетом вероятности угадывания всех шести чисел, попытаемся оценить среднюю величину выигрыша I категории. Предположим, что выигрыш I категории в игре ЛОТТО «МИЛЛИОН» составляет 10.000.000 рублей. Для подсчета среднего выигрыша I категории следует эту величину выигрыша умножить на вероятность. В результате средняя величина выигрыша I категории, приходящаяся на 1 билет, составляет
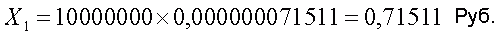
или где-то около 72 копеек. Следовательно, из ваших 30 рублей, потраченных на покупку билета, в среднем где-то около 72 копеек уходит на покрытие выигрышей I категории. А куда же уходят остальные деньги?
Не следует, однако, забывать, что есть еще выигрыши II и III категории. Перейдем к оценке среднего выигрыша II категории, когда угадано 5 чисел, то есть 5 чисел попадает в «счастливую» область, а 1 число — в «несчастливую» область. Сколькими способами можно реализовать это случайное событие? Для подсчета этого числа обратим внимание, что 5 чисел в «счастливой» области можно выбрать
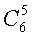
способами, а 1 число в «несчастливой» области

, поэтому количество способов, которыми можно угадать 5 чисел, равно
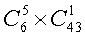
. Значение каждого из сомножителей легко определить, и число возможных комбинаций, благоприятных для угадывания 5 чисел, — m = 6 х 43 = 258. Полное же число всех возможных комбинаций при отборе 6 чисел из 49, как и раньше,
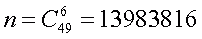
. Окончательно для вероятности угадать 5 чисел из 49 получим следующее значение
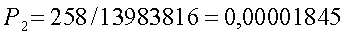
Если же принять теперь, что величина выигрыша II категории составляет 100.000 рублей, то средняя величина выигрыша, приходящаяся на 1 билет, оказывается равной
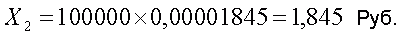
Остается теперь оценить среднюю величину выигрыша III категорий. Рассуждая аналогичным образом, легко определить, что число комбинаций, благоприятных для угадывания четырех чисел, определяется произведением
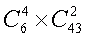
и, следовательно, m = 15 х 903 = 13545. Вероятность выигрыша III категории
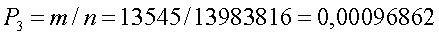
Предположим теперь, что выигрыш третьей категории составляет 10000 рублей. Тогда средняя величина выигрыша, приходящаяся на один билет, будет равна
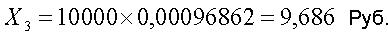
Полная же средняя величина выигрыша, приходящаяся на 1 билет, складывается из выигрышей I, II и III категорий:
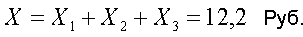
Следовательно, в рассмотренном нами случае из 30 рублей, затраченных вами на покупку билета, меньшая часть в среднем в объеме 12,2 рубля уходит на покрытие выигрышей, а большая часть в объеме 17,8 рублей присваивается организаторами лотереи. Условия этой игры можно считать справедливыми, если эти присвоенные 17,8 рублей действительно полностью уходят на цели, перечисленные выше.
Таким образом, если вы придерживаетесь простой системы игры, то из затраченных вами 30 рублей на покупку билета приблизительно 2% идут на выплату выигрышей I категории, 6% — выигрышей II категории и 32% — выигрышей III категории, если выигрыши по этим категориям составляют соответственно 10 млн., 100 тыс. и 10 тыс. рублей.
А как обстоит дело, если выбрана более сложная система игры, например, развернутая? Отличаются ли в этом случае вероятности и средние величины выигрышей?