ГЛАВА III — часть 2
Комбинации… комбинации...
А сколько вариантов будет при числе подходов четыре или пять? Особый интерес для нас представляет случай, когда число подходов равно шести или больше, потому что именно этот случай полностью соответствует условиям игры ЛОТТО «МИЛЛИОН». Нетрудно убедиться, что полное число вариантов различных подходов соответствующей игры с n подходами равно 2**n(2 в степени n). Действительно, при одном подходе (n=1) возможны два варианта («угадал» или «не угадал»), так как 2**n=2**1=2. При числе подходов n=2, полное число вариантов равно 4 («угадал + угадал». «угадал + не угадал», «не угадал + угадал», «не угадал + не угадал») в соответствии с предложенной нами формулой 2**n=2**2=4. Как мы убедились выше, при трех подходах число возможных вариантов равно 8, что также согласуется с формулой 2**n=2**3=8. Продолжая эту цепь рассуждений, можно найти полное число возможных вариантов для четырех подходов 2**n=2**4=16, для пяти подходов 2**n=2**5=32 и т.д.
Смысл такой закономерности очевиден и причина ее состоит в том, что при увеличении числа подходов на единицу, каждый из вариантов, возможных для данного числа подходов, превращается в новые два варианта, соответствующие возможным исходам в новом подходе «угадал» или «не угадал», и тем самым полное число возможных исходов удваивается.
Следует, однако, отметить, что при числе подходов больше шести вышеприведенное рассуждение становится не вполне корректным, поскольку при условиях, принятых в игре ЛОТТО «МИЛЛИОН», невозможно угадать более шести цифр, и поэтому сформулированное нами простое правило 2**n срабатывает, только когда число отмеченных чисел не превышает шести.
А как же подсчитать правильно число различных вариантов, когда число отмеченных чисел больше шести? Ответить на этот вопрос, впрочем, как и на любой другой, можно двумя способами. Первый из них состоит в том, чтобы сказать: «Посмотри таблицу такую-то и там найдешь то, что тебе нужно, или выучи правило такое-то и, действуя в соответствии с ним, достигнешь того, что тебе нужно».
Второй способ требует больших усилий, но приводит к пониманию принципов формирования таблиц и формулирования правил и позволяет в случае необходимости их составить самостоятельно.
В соответствии с первым способом предлагаем вашему вниманию Таблицу 1, в которой сведены все данные для подсчета количества различных вариантов, когда в билете отмечено от 1 до 11 чисел. При желании каждый из вас может легко продолжить эту таблицу, если воспользуется следующим простым правилом: каждое число, стоящее в последней строке, сложите со следующим за ним и поместите эту сумму под вторым слагаемым в следующей строке. Направление этих действий схематически показано в Таблице 1.
Таблица 1. Количество различных вариантов исхода игры в зависимости от
числа отмеченных чисел в билете ЛОТТО «МИЛЛИОН»
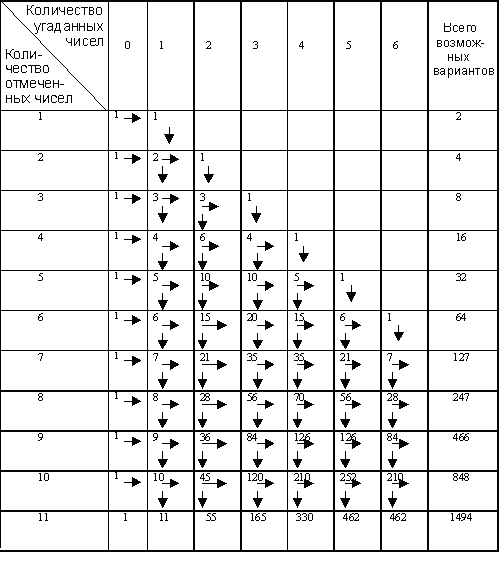
Если бы мы эту таблицу не ограничивали справа, а увеличили неограниченно число колонок, то сумма всех возможных вариантов в каждой строке оказалась бы равной 2**n, где n — номер строки. Для первых шести строк это правило выполняется, а все строки, начиная с седьмой, оказываются неполными, и поэтому сумма возможных вариантов в них меньше, чем 2**n.
Таблица 1 с древних пор была известна математикам, и хотя в настоящее время ее называют треугольником Паскаля — по имени французского математика Блеза Паскаля, жившего в 1623-1662 годах, его уже знал живший в 1500-1557 годах итальянский математик Тарталья, а еще раньше этот треугольник встречался в работах арабских математиков Гиясэддина и Омара Хайяма.
Попробуем теперь разобраться, как же получаются эти загадочные числа в треугольнике Паскаля. Для этого рассмотрим простой пример. Предположим, что мы отметили в билете ЛОТТО «МИЛЛИОН» шесть произвольных чисел и хотим узнать, сколько существует вариантов, в которых будет угадано 4 цифры из 6. Согласно Таблице 1, таких вариантов существует 15. Как получается это число?
Для того, чтобы ответить на этот вопрос, обратимся снова к Рис.3, на котором «счастливыми» являются номера 12, 14, 18, 23, 30 и 36. Число способов, которыми можно угадать 4 из этих 6 номеров. математики называют числом сочетаний и обозначают его
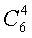
. Эта запись читается так: «число сочетаний из шести по четыре». Определить его величину можно с помощью следующих рассуждений.
Предположим, что угаданы числа 12, 14, 30 и 36. Сколько вариантов существует для такого угадывания? Число 12 может быть угадано в любой из 6 попыток, то-есть может быть названо 1-м, 2-м, 3-м, 4-м, 5-м или 6-м. Следовательно, для угадывания числа 12 существует 6 различных вариантов. Второе число 14 может быть угадано в любой из оставшихся пяти попытках, следовательно, для его угадывания имеется 5 различных вариантов. Продолжая эти рассуждения, легко прийти к выводу, что для угадывания числа 30 существует 4 различных варианта, а числа 36 — 3 варианта. Следовательно, для угадывания четверки чисел из шести «счастливых» существуют всего 6х5х4х3 вариантов.
Но не все эти варианты различны. Предположим, что эти числа были угаданы в первых же четырех попытках. Тогда все эти варианты, соответствующие различной последовательности заполнения «счастливых» номеров в тех же самых попытках (всего 24 варианта), фактически представляют 1 вариант (число перестановок 4 элементов равно 4х3х2х1=24).

Окончательно для искомого числа сочетаний мы получили формулу:
Эта формула для числа сочетаний является справедливой и при любых других количествах отмеченных чисел и количествах «угаданных». В общем случае можно сформулировать следующее правило: для того, чтобы определить количество возможных вариантов с m угаданными числами для отмеченных n чисел, необходимо вычислить число сочетаний
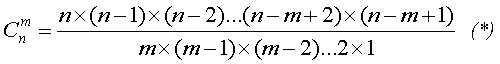
В этой формуле число сомножителей в числителе и знаменателе одинаково и равно m. Формула (*) известна математикам давно, с тех пор, как в XVI веке были заложены основы новой области математики, названной комбинаторикой. Комбинаторика отвечает на вопрос о том, сколько различных комбинаций, подчиняющихся определенным условиям, можно составить из заданных объектов. В настоящее время комбинаторные методы широко используются для решения транспортных задач, составления расписаний и планов производства и реализации продукции.
Но первоначально комбинаторные задачи были сформулированы для азартных игр в карты, кости, лото, солитер и др. И применение комбинаторных методов для решения именно этого класса задач для нас наиболее существенно. Имеется много различных комбинаторных формул, однако для наших целей вполне достаточно одной только формулы (*). С ее помощью мы можем проанализировать и количество возможных комбинаций, и вычислить вероятности различных исходов игры, и оценить вероятные финансовые результаты игры. Но все это чуть позже.
А сейчас вернемся к Таблице 1 и попробуем понять, как получаются те числа, которые заполняют ее строки. Согласно сформулированному выше правилу, чтобы заполнить клеточку в таблице в строке n и в столбце m, необходимо вычислить число сочетаний
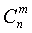
. Так например, если мы отметили 11 чисел и хотим найти количество комбинаций, соответствующих 5 угаданным числам (то есть заполнить в Таблице 1 строку 11 и столбик 5), необходимо вычислить
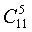
. Согласно формуле (*) и в числителе, и в знаменателе должно быть по 5 сомножителей
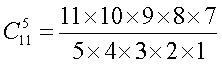
Можно, конечно, перемножить все числа в числителе и этот результат запомнить, затем перемножить все числа в знаменателе и разделить первый результат на второй. Но так поступают только те, кто очень любит делить и умножать. А если вы ленивы, и вам этого делать не хочется, то лучше сократить в числителе и знаменателе все, что можно, получить результат, затратив значительно меньше усилий, и убедиться, что он совпадает с соответствующим значением в таблице.
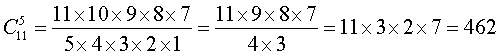
Потратив немного времени, мы теперь можем составить Таблицу 2 для полного числа различных выигрышных вариантов игры ЛОТТО «МИЛЛИОН». Каждая строка этой таблицы соответствует определенному количеству, отмеченных чисел n в билете от 6 до 49. Во втором столбце таблицы указано количество различных «шестерок», которые можно составить из отмеченных чисел, равное
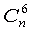
. Например, если вы отметили в билете 10 чисел, то из этих десяти отмеченных чисел можно составить 210 различных «шестерок»:
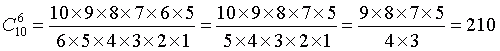
То есть, если вы в билете отметили 10 чисел, то по отношению к возможному выигрышу суперприза (угадано 6 чисел) это эквивалентно тому, что вы отметите в 210 различных билетах по 6 чисел, и поэтому естественно, что стоимость такого заполненного билета будет уже не 30 рублей, а 30х210=6300 рублей. Но сколько при этом будет сэкономлено бумаги и времени на заполнение билета! А если говорить серьезно о преимуществах такого способа заполнения билета, то следует обратить внимание на количество выигрышных вариантов II и III категории, приведенных в следующих столбцах таблицы и сопровождающих выигрыш суперприза. Выигрышные варианты II категории (угадано 5 чисел) и III категории (угадано 4 числа) всегда присутствуют в билетах, выигравших суперприз, если количество отмеченных чисел в билете (n) больше шести. Легко получить формулы для вычисления количества выигрышей второй и третьей категории. Если вы угадали 6 цифр, то количество выигрышей II категории, сопровождающих выигрыш суперприза, равно 6x(n-6), а количество выигрышей третьей категории.
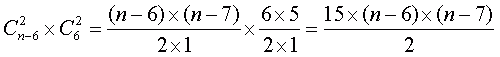
В Таблице 2 числа в четвертом столбце были получены с помощью первой из этих формул, а в пятом столбце — по второй формуле.
Если вы угадали 5 цифр, то количество возможных выигрышных вариантов II категории равно n-5, а третьей категории.
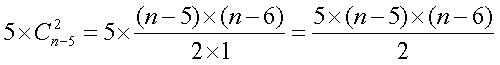
С помощью этих формул заполнены шестой и седьмой столбцы Таблицы 2.
Наконец, если среди n отмеченных чисел оказалось 4 выигрышных, то количество выигрышных вариантов III категории (четверок) равно числу двоек, которые можно сформировать из неугаданных номеров, то-есть
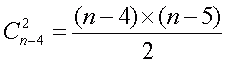
Эта формула была использована при заполнении последнего столбца Таблицы 2.