ГЛАВА III
Комбинации… комбинации...
Прежде чем перейти к обсуждению способа подсчета вероятности угадывания двух, трех и более карточек, рассмотрим одну из наиболее простых задач теории вероятностей, которая включает в себя все наиболее существенные особенности, возникающие при подсчете вероятностей в более сложных задачах.
Предположим, что из колоды, состоящей из 10 карточек, представленной на Рис.1, на восьми из которых написана цифра «5», а на двух — «3», вынимаются 2 карточки. Требуется оценить вероятность, что обе вынутые карточки будут иметь цифру «3».
Решение этой задачи можно получить двумя способами. Первый состоит в том, чтобы составить таблицу всех возможных исходов (Рис. 2) и выделить черным цветом те варианты, которые соответствуют случаю, когда обе вынутые карточки имеют цифру «3». Последнее имеет место, если будут вынуты карточки №4 и №8 или №8 и №4. Из таблицы исключены варианты, которые стоят на диагонали, описывающие невозможный исход игры, когда обе вынутые карточки имеют одинаковые номера. Общее число возможных исходов здесь равняется 90 (полное число незаштрихованных клеток), а число благоприятных исходов — 2 (число черных клеток). Таким образом, согласно правилу, сформулированному выше, вероятность того, что обе вынутые карточки будут содержать цифру «3», равна 2/90 или 1/45.

Рис.2 Таблица возможных элементарных исходов при извлечении двух карточек
Этот же результат можно получить другим, более простым способом, если рассуждать следующим образом. Чтобы выиграть, необходимо вынуть два раза подряд карточку с числом «3». Вероятность того, что первая карточка будет иметь цифру «3», равна 2/10 или 1/5, поскольку среди 10 карточек в колоде 2 имеют цифру «3». После того как была вынута из колоды одна карточка с цифрой «3», в колоде осталось всего 9 карточек, и лишь 1 из них имеет цифру «3». Следовательно, вероятность того, что вторая вынутая карточка будет иметь цифру «3», равна 1/9. Для вычисления же полной вероятности того, что обе карточки будут иметь цифры «2», надо перемножить эти два значения и получить 1/5 х 1/9 = 1/45.
Рассмотрим теперь задачу, более близкую к нашим интересам. А эти интересы в данном случае связаны с подсчетом вероятностей угадывания цифр в розыгрышах ЛОТТО «МИЛЛИОН». По правилам этой игры, требуется угадать шесть отобранных (счастливых) «карточек» из общего количества имеющихся в наличии сорока девяти. Для наглядности заштрихуем «счастливые карточки», как это показано на Рис.3.
Наша цель состоит в «угадывании» этих заштрихованных карточек, и чем большее их число мы угадаем, тем лучше. Представьте себе, что все 49 карточек перевернуты рубашками вверх, и вы наугад пытаетесь указать, какая из карточек заштрихована. После этого вы переворачиваете выбранную карточку цифрой вверх
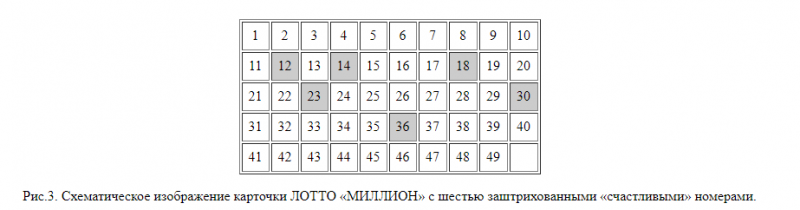
Рис.3. Схематическое изображение карточки ЛОТТО «МИЛЛИОН» с шестью заштрихованными «счастливыми» номерами.
Какова вероятность того, что перевернутая карточка окажется заштрихованной? Очевидно, она и в этом случае равна отношению числа благоприятных для нас исходов (заштрихованных карточек, а их число равно 6) к полному числу всех возможных исходов (то есть полному числу карточек, число которых 49). Таким образом, вероятность угадать одну из шести отобранных карточек равна 6/49, а вероятность не угадать, соответственно — 43/49.
Рассмотрим теперь, как распределены вероятности при попытке угадать две из шести отобранных карточек. Если вы угадали две карточки, значит вы попали оба раза в область «заштрихованных карточек». Как мы уже знаем, вероятность угадать одну карточку при одном подходе равна 6/49. Но после того как была угадана первая карточка, ее можно считать уже устраненной из рассмотрения. Полное число карточек, оставшихся в колоде, станет равным 48, а «заштрихованных» — 5. Поэтому вероятность того, что вторая карточка будет угадана, равна 5/48. Полная же вероятность угадать две карточки при двух подходах равна (6/49) х (5/48) = (6х5)/(49х48) .
При двух подходах возможны еще два других исхода — либо будет угадана только одна карточка, либо ни одной. Аналогичным образом могут быть рассчитаны вероятности и этих исходов. Так, например, вероятность не угадать обе карточки равна произведению того, что не будет угадана первая карточка (43/49), на вероятность того, что и вторая карточка также не будет угадана (42/48), то есть (43/49)х(42/48) = (43х42)/(49х48).
Для подсчета вероятности угадывания одной карточки при двух подходах следует учесть возможность существования двух различных вариантов, приводящих к одинаковому исходу. Эти два варианта можно кратко сформулировать так: «угадал — не угадал» и «не угадал — угадал». Вероятность первого варианта равна (6/49)х(43/48), а второго — (43/49 )х( 6/48). Полная же вероятность угадать одну карточку при двух подходах оказывается равной
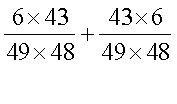
Если сложить теперь вероятности всех трех возможных исходов, то, как и следовало ожидать, сумма всех вероятностей окажется равной 1. Конечно, хоть что-нибудь, но должно же случиться с достоверностью (то есть с вероятностью 100%). Как говорят, уж если не выиграю, то проиграю.
Из приведенных рассуждений видно, что количество возможных вариантов различных исходов игры быстро растет с увеличением числа подходов. Так, например, при трех подходах возможны следующие варианты.
Угаданы все три карточки:
1) угадал + угадал + угадал: вероятность =
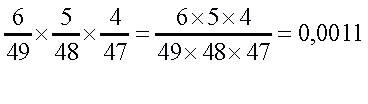
Угаданы две карточки из трех:
2) угадал + угадал + не угадал: вероятность =
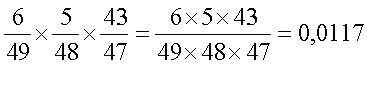
3) угадал + не угадал + угадал: вероятность =
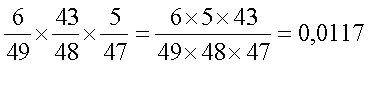
4) не угадал + угадал + угадал: вероятность =
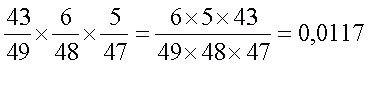
Угадана одна карточка из трех:
5) угадал + не угадал + не угадал: вероятность =
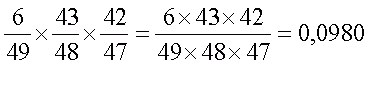
6) не угадал + угадал + не угадал: вероятность =
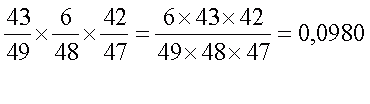
7) не угадал + не угадал + угадал: вероятность =
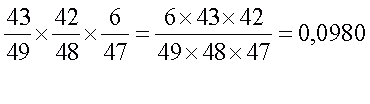
Не угадана ни одна карточка:
8) не угадал + не угадал + не угадал: вероятность =
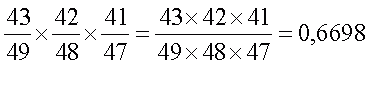
Нетрудно убедиться, что и в этом случае сумма вероятностей равна 1.