ГЛАВА II
Не упустите свой шанс!
В повседневной жизни мы все пользуемся словами «маловероятный», «вероятный», «достоверный». Например, мы можем сказать, что возможность дождя маловероятна или вероятность дождя очень большая. Иногда может использоваться более конкретная формулировка с выражением вероятности в процентах, когда говорят, что такое-то событие может произойти с вероятностью столько-то процентов. При этом подразумевают, что событие невозможное происходит с вероятностью ноль процентов, событие достоверное с вероятностью — сто процентов, а вероятность любого случайного события лежит между этими двумя значениями.
Что же мы подразумеваем под этим интуитивным понятием вероятности? С точки зрения математики возможны две различные интерпретации этого сугубо абстрактного понятия. В первой из них понятие вероятности ассоциируется с частотой появления данного события в серии опытов, в каждом из которых анализируемое событие может появиться или не появиться. Такое событие математики называют случайным. Рассмотрим в качестве примера простейший вариант игры «Угадайка». Пусть имеется 10 карточек, на которых написана, или цифра «5», или цифра «3». Пусть на 8 карточках написана цифра «5», а на 2 карточках цифра «3» (Рис.1)

Рис.1 Карточки для игры «Угадайка»
В процессе игры эти карточки перетасовываются и игроку предстоит из этой колоды карточек вынуть карточку с цифрой «3». Случайное событие А, вероятность которого необходимо определить, состоит в том, что игрок «угадал». Предположим теперь, что была произведена серия из 20 опытов и игрок угадал 3 раза. Тогда говорят, что частота появления события А составляет 15 процентов:
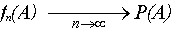
Здесь буква f выбрана по той причине, что она является первой буквой в слове frequency, что в переводе с английского языка означает «частота». «Ну и что?» — можете спросить вы, — «Если я проведу другую серию из 50, 70 или 100 опытов, эта частота может принять значения и 20% и 10% и, возможно, любое другое значение!». На самом деле это не так. Существует определенный закон, справедливость которого доказывается в теории вероятностей, и этот закон называется законом больших чисел, согласно которому в любой серии опытов при увеличении их числа частота появления случайного события всегда стабильно стремится к одной и той же величине и это предельное значение можно принять за вероятность Р(А) (probability — на английском языке):
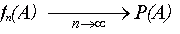
Таким образом, согласно этому утверждению, чтобы найти вероятность выигрыша в игре «Угадайка», нужно провести достаточно длинную серию опытов и полученную частоту выигранных партий, выраженную в процентах, принять за вероятность. Конечно, такой способ определения вероятности является вполне конструктивным, но если учесть, что в нашей жизни за все приходится платить, — очень уж дорогим.
А нельзя ли определить вероятность выигрыша априори, то есть до начала опытов? Оказывается, что в ряде случаев это возможно, например, для рассматриваемой нами игры «Угадайка». Метод, который используется для априорного определения величин вероятности, основан на втором возможном варианте ее интерпретации и состоит он в следующем. Исход каждой партии, состоящий в том, что игрок выбирает одну из десяти возможных карточек, рассматривается как некоторая реализация в пространстве возможных элементарных событий. В данном случае это пространство состоит из 10 карточек, представленных на Рис.1. Все эти события можно разбить на две группы — «благоприятные» для А, их число обозначим буквой m, когда цифра на карточке совпадает с заданной цифрой «3», и «неблагоприятные» для А, когда эта цифра с ней не совпадает. На Рис. 1 «неблагоприятные» события заштрихованы и их число равно 8, а «благоприятные» для А — не заштрихованы и их число равно 2. Обозначим буквой n полное число возможных элементарных событий, а буквой m — число благоприятных для события А. В нашем случае n=10, а m=2. Тогда согласно второму определению вероятности
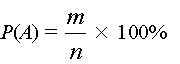
то — есть вероятность появления события А равна отношению числа благоприятных событий для А к полному числу возможных элементарных событий, выраженному в процентах. Согласно этому определению, вероятность выигрыша в игре «Угадайка» составляет 20%, и эту величину мы нашли, не проводя никакой серии экспериментов.
Хорошо, а какая нам польза от того, что мы знаем величину вероятности выигрыша в игру «Угадайка»? Оказывается, очень большая, — и состоит она в том, что мы можем установить справедливые денежные условия, если хотим превратить эту игру в азартную. И уж, во всяком случае, если эти условия установлены кем-либо другим, для нас теперь не составит труда определить, являются ли они справедливыми. В частности, если стоимость каждой партии равняется 10 рублям, то для оплаты 30 партий игры игроку придется внести 300 рублей. Поскольку вероятность выигрыша в каждой партии равна 20%, то среднее число выигранных партий составит 30х20/100=6 партий. Следовательно, чтобы компенсировать затраченные 300 рублей за 6 выигранных партий, необходимо, чтобы выигрыш в каждой из них составлял 50 рублей. Если же выигрыш при этих условиях был бы меньше 50 рублей, то условия игры можно было бы считать несправедливыми, а при выигрыше больше 50 рублей — очень выгодными.
Теперь вам, надеемся, понятно, как использовать известные вероятности выигрыша для оценок возможных исходов азартной игры. Предположим, что в каждой партии вероятность выигрыша составляет p %, и вы сыграли n партий. За участие в каждой из партий вы заплатили l рублей. Если за каждую выигранную партию вы получаете s рублей, то ваш наиболее вероятный выигрыш составит
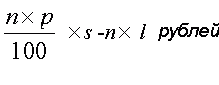
Пример. Пусть вероятность выигрыша в каждой партии составляет 15%. Стоимость каждой игры 10 рублей. Выигранная партия приносит доход 70 рублей. Определить вероятный выигрыш после ста сыгранных партий.
1) Вероятное число выигранных партий
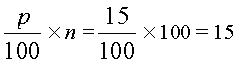
2) Доход от выигранных партий
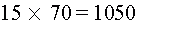
3) Затраты на игру
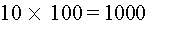
4) Вероятный выигрыш
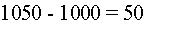
.
Стоит ли тратить время и средства на то, чтобы за 100 партий выиграть 50 рублей? Хотя вопрос этот и не праздный, но в некотором смысле он лишен содержания, поскольку относиться к категории вопросов типа «А стоит ли жить, если все равно умрем?». Ведь проведенная оценка вовсе не означает, что будет выиграно именно 50 рублей. Речь шла о средней (или вероятной) величине выигрыша. А может быть, вы относитесь к той категории людей, которым очень уж сильно везет, и серия выигранных партий будет значительно больше 15? Во всяком случае, каждый из нас, принимая участие в азартной игре, надеется на это. Однако, сколь бы ни была глубокой наша надежда, это не избавляет нас от необходимости знания наиболее реалистичных возможных исходов игры. Знание нас всегда обогащает, а незнание — не освобождает от ответственности — таков неумолимый приговор судьбы!
Рассмотренный нами пример показывает, как важно знать величину вероятности выигрыша. Приведенные выше способы ее оценки так же хороши, как и любой совет. Каждый из нас, получив его, вроде бы и знает, что надо делать, но не знает как. И необходима еще добрая сотня советов, чтобы знать, как претворить в жизнь первый из них. Именно такая ситуация складывается с подсчетом вероятностей. В принципе, ясно, что вероятность — это отношение числа благоприятных к общему числу возможных исходов, выраженная в процентах, но как подсчитать число этих исходов в более сложных играх, чем описанная выше игра «Угадайка». Даже при небольшом усложнении этой задачи, когда надо угадать не одну карточку, а хотя бы две, такой подсчет покажется для неискушенного человека довольно сложной задачей. А в игре ЛОТТО «МИЛЛИОН» надо угадать сразу шесть «карточек». Как же подсчитать вероятности в более сложных играх?